Visual geometry May26

 

19-gon

Tessellation

30-gon and pentagons

Visual Geometry February26

Visual Geometry Jan26

Geo Dec25

 

Geo Nov25

17-gons

17-gon

Triangular nested grids

Triangular nested grids:

3,3,3,3... or 5,5,5,...

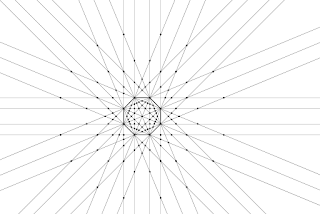
Visual representation of Fermat numbers

 Images that show a visual representation of Fermat numbers and how those images can be used to create tessellations and other types of mathematical art.

The images are a combination of  visual geometry and visual number theory with an art component.

The images are based on square grids. 

The starting point for the Fermat numbers (3,5,17,257...) is a 3x3 square grid.

Geo Oct25, visual geometry

 

7,9,13,21...

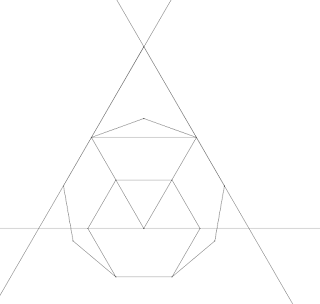
27-gon neusis construction

 The construction of a 27-gon is based on the general construction methods for 6n+3 polygons.

Starting with the nonagon, 18-gon (double the nonagon) , and we can find the defining lines to construct the 27-gon.

27-gon neusis construction

Visual Geometry Sept 25

5,13,125,15133

Generalized Fermat Numbers, visualized

3,5,17 Fermat numbers, visualized

 

Geo June25

Visual geometry, april/may 2025

 

Visual geometry Feb/ March 25

Squares fitted in regular polygons

The process I initially follow , is to start with the regular polygon that I want to insert the squares in, draw a loose point in one of the sides and repeat on the other sides (same length). I draw the squares and move the original point until I find the meeting point of the squares. I use GeoGebra to make the drawings.

6n+3 series, visual geometry

 Nonagon

6n+3 series, visual geometry

Visual geometry Jan25

Visual geometry Nov-Dec24

 

8,24,56,120,248,504,1016,2040,4088,8184,16376

,32760...

Visual geometry Aug-Sep 24

Visual geometry July24

Visual geometry June24

Squares and pentagons

3d geometry: heptagon

 A geometric template to create a 3d geometric figure based on the heptagon:

A 3d shape created with heptagons

Visual geometry May 24

Geometric sphere

Square root 3 and 2

 Nonagons and hexagons circular expansion:

(6n+7)*3

 (6n+7)*3

14,21

(6n+3)*3 series

(6n+3)*3 series

(6n+5)*3 series

 (6n+5)*3 series

CUBES

 

CUBES

Pentagons and squares filling of the plane

 Pentagon and square filling of the plane,

Pentagon and 1/2 square root 3

 

Numbers:

Phi: (√(5) + 1) ÷ 2

1.53884176859

0.19320903898

0.09318924785

Nonagons (6n+3)

 

21-gons (6n+3)

 

The 6n+3 series

 What do the numbers 3,9,15,21,27,33,39,45,51,57,63,69,75,81,87,93,99... when it comes to regular polygons have in common?

Construction of a nonagon with compass and marked ruler

 A visual construction of a regular nonagon with compass and marked ruler (neusis construction of a nonagon).

Start with a hexagon and triangle as a base, 

Filling of the plane with pentagons and hexagons

Filling of the plane with pentagons and hexagons

11-gon and triangle

 

Mapping of regular polygons: octagon

 

√2+1 lines, one being the side of 
the regular octagon.

√ 2

√ 2

 a2 + b2 = c2.
(√ 2+1)2 +(1)2 = c2

Lines of one

 a2 + b2 = c2.
(√2/2)2 + (√2/2+1)2 =c2

Lines of 2